fontaine.mws
Alexis
Fontaine's solution to St. Petersburg problem
24
February 2003
Pierre
promises to pay
Paul 1 écu if he brings forth heads on the toss of a coin, 2
écus
if he brings forth heads only on the second toss of a coin, and in
general,
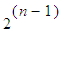 écus if he
brings forth heads only
on the n th
toss of the coin. The problem is to determine the stake of Paul which
makes
the game fair.
écus if he
brings forth heads only
on the n th
toss of the coin. The problem is to determine the stake of Paul which
makes
the game fair.
Let
x be
the
wealth of Pierre and let y
be the stake of Paul. It is assumed that
Pierre
puts all of his wealth into the game. The total funds in the game is
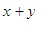 .
.
Fontaine
notes that
the payoff must be bounded by the wealth of Pierre. Indeed, for this
reason
there exists an integer N
such that if Paul has not brought forth
heads
by the N th
toss, his payoff can be no greater than
x . It
follows
that N
satisfies
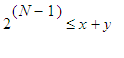 and
and
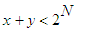 .
.
If
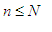 , the gain of Paul is
, the gain of Paul is
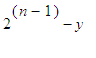 with probability
with probability
 . Otherwise, for
. Otherwise, for
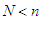 , the gain of Paul is
x with
probability
, the gain of Paul is
x with
probability
 . Therefore the expected gain of
Paul is
. Therefore the expected gain of
Paul is
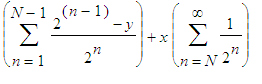 .
.
Call
this expectation
A. We have
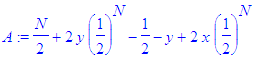
In a
fair game this
expectation is 0. By the condition above,
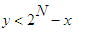 . Therefore, solving A
for
y and
making
use of this condition, we have
. Therefore, solving A
for
y and
making
use of this condition, we have

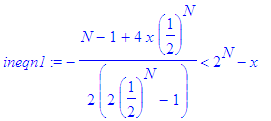
Simplifying,
we obtain
that x
is bounded above by
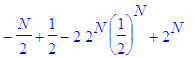
This
reduces to the
bound UB where
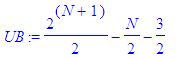
By
the other condition
on N ,
we have that x
is bounded below by
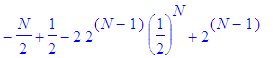
This
reduces to the
bound LB where

If
we substitute, say,
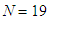 , we find that if the
wealth of Pierre is bounded
by 262134 and 524277.
, we find that if the
wealth of Pierre is bounded
by 262134 and 524277.
![[262134, 524277]](images/fontaine20.gif)
and
for the lower bound
of x
we have the corresponding
y of
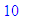
Similarly,
if we substitute
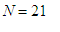 ,
,
![[1048565, 2097140]](images/fontaine23.gif)
Now,
assuming
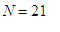 and
and
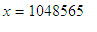 , we obtain
y
, we obtain
y
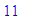
Consequently,
we find,
as did Fontaine, that if Pierre can put 1,048,565 écus into the
game,
then Paul must put in 11 écus. The game must end at the 21st
toss
because if Paul has not cast a heads by this time, then Pierre must
give
him all his wealth.
If
Pierre can put in
262,134 écus, then Paul must put in 10. The game must end at the
19th
toss.
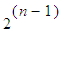 écus if he
brings forth heads only
on the n th
toss of the coin. The problem is to determine the stake of Paul which
makes
the game fair.
écus if he
brings forth heads only
on the n th
toss of the coin. The problem is to determine the stake of Paul which
makes
the game fair.
![]() , we find that if the
wealth of Pierre is bounded
by 262134 and 524277.
, we find that if the
wealth of Pierre is bounded
by 262134 and 524277.
![]() and
and
![]() , we obtain
y
, we obtain
y