 |


b. London, England 29 October 1656
d. Greenwich, England 14 January 1743
Edmond Halley, born into a wealthy family, was tutored at home until being sent first to St. Paul's School and then, at age 17, to Queen's College, Oxford. At age 22 he received an MA degree from Oxford.
Halley was elected to the Royal Society in 1678. He edited the Philosophical Transactions of the Royal Society from 1685 to 1693. He obtained the Savilian chair of geometry at Oxford in 1704, was appointed astronomer royal in 1720, and elected to the Acadèmie Royale des Sciences at Paris in 1729. Of course, he is most famous for having computed the orbit of the comet named after him.
Many members of the Royal Society had been anxious for records suitable for construction of a life table. Their request was finally answered in 1693 with publication of the Breslau table.
Caspar Neumann (1648–1715) had studied for the ministry. In 1678, he became deacon at St. Mary Magdeline in Breslau, Silesia. Records had been kept in Breslau concerning age, sex, year and month of death for many years. Neumann examined the records beginning with the year 1687 and sent his observations to Gottfried Leibnitz who in turn informed Justell, Secretary of the Royal Society of their existence. The secretary wrote a request to Neumann who then forwarded his data for the years 1687 to 1691. The Royal Society asked Edmund Halley to analyze the data. Halley published his researches in 1693 in the paper An Estimate of the Degree of the Mortality of Mankind.
Under the assumption that the population of Breslau had been a stationary population for many decades, Halley concluded that a table which displayed the number of people at each age must also display the chances of mortality at each age. An analysis of the Breslau data permitted Halley to construct the following table. This table shows the number of individuals living at each age. Thus, for example, there are 1000 children of age 1.
|
Age |
No. |
Age |
No. |
Age |
No. |
Age |
No. |
Age |
No. |
Age |
No. |
|
1 |
1000 |
15 |
628 |
29 |
539 |
43 |
417 |
57 |
272 |
71 |
131 |
|
2 |
855 |
16 |
622 |
30 |
531 |
44 |
407 |
58 |
262 |
72 |
120 |
|
3 |
798 |
17 |
616 |
31 |
523 |
45 |
397 |
59 |
252 |
73 |
109 |
|
4 |
760 |
18 |
610 |
32 |
515 |
46 |
387 |
60 |
242 |
74 |
98 |
|
5 |
732 |
19 |
604 |
33 |
507 |
47 |
377 |
61 |
232 |
75 |
88 |
|
6 |
710 |
20 |
598 |
34 |
499 |
48 |
367 |
62 |
222 |
76 |
78 |
|
7 |
692 |
21 |
592 |
35 |
490 |
49 |
357 |
63 |
212 |
77 |
68 |
|
8 |
680 |
22 |
586 |
36 |
481 |
50 |
346 |
64 |
202 |
78 |
58 |
|
9 |
670 |
23 |
579 |
37 |
472 |
51 |
335 |
65 |
192 |
79 |
49 |
|
10 |
661 |
24 |
573 |
38 |
463 |
52 |
324 |
66 |
182 |
80 |
41 |
|
11 |
653 |
25 |
567 |
39 |
454 |
53 |
313 |
67 |
172 |
81 |
34 |
|
12 |
646 |
26 |
560 |
40 |
445 |
54 |
302 |
68 |
162 |
82 |
28 |
|
13 |
640 |
27 |
553 |
41 |
436 |
55 |
292 |
69 |
152 |
83 |
23 |
|
14 |
624 |
28 |
546 |
42 |
427 |
56 |
282 |
70 |
142 |
84 |
20 |
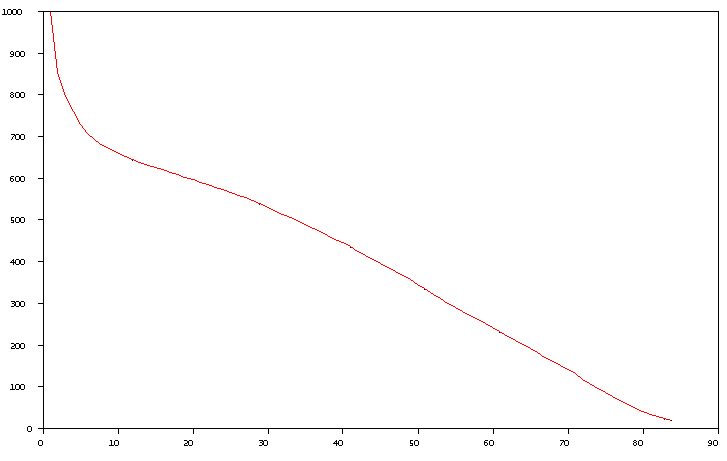
The number living by year is plotted below. It should be noted how strikingly different a correct life function differs from that conjectured by Graunt. Also note the terrible toll taken by infant mortality.
 |
There are some inconsistencies. Halley supposed that there are 1238 births annually in Breslau. Of these, 348 died within the first year of life leaving only 890 to achieve one year of age. Notice that he has 1000 living at age 1 instead. In addition, another 198 died in the five years between age 1 and age 6. Therefore, only 692 survived to age 6. He has 710. If we wish to preserve the ratio of number living at age 6 to number of births, that is the ratio of 692 to 1238, then we must take the number of births to be 1270.
Another problem is that Halley did not give a maximum lifetime. Note there yet remain 20 survivors at age 84. It seems to have been customary when using the Breslau table to assign 0 survivors to age 86.
With the considerations given above, Halley's table can be collapsed so as to correspond to that of Graunt.
|
Age |
0 |
6 |
16 |
26 |
36 |
46 |
56 |
66 |
76 |
86 |
|
Number living |
1270 |
710 |
622 |
560 |
481 |
387 |
282 |
182 |
78 |
0 |