recherch_x.html
recherch_x.mws
Recherches sur
l'intégration des équations différentielles aux
différences finies, et sur leur usage dans la théorie des
hasards.
P.S. Laplace
PROBLEM
X.
If in a pile of
x pieces one
takes a number
at random, it is necessary to determine the probability that this
number
be even or odd .
Let
y denote
the sum of
the even cases, z
the sum of the odd.
>
restart:
>
eqn1:=y(x+1)=y(x)+z(x);
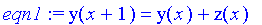
>
eqn2:=z(x+1)=z(x)+y(x)+1;
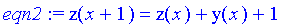
If there is but 1
piece
(
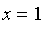 ), then we have the
initial conditions
), then we have the
initial conditions
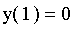 and
and
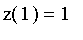 . The solution is
therefore
. The solution is
therefore
>
rsolve({eqn1,eqn2,y(1)=0,z(1)=1},{y,z});
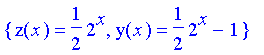
Now, since
y is
smaller than
z ,
it is clear
that the odds are favored. The probability of even is
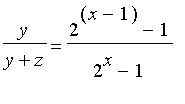 .
.
>
>
![]() ), then we have the
initial conditions
), then we have the
initial conditions
![]() and
and
![]() . The solution is
therefore
. The solution is
therefore
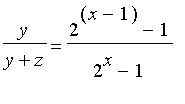 .
.