recherch_xi.mws
Recherches sur
l'intégration des équations différentielles aux
différences finies, et sur leur usage dans la théorie des
hasards.
P.S. Laplace
PROBLEM
XI.
Let a
be a sum which Paul constitutes to an
annuity, in
a way that the interest is
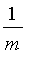 of that which is due
to him: I suppose that, for some arbitrary reasons, one keeps each year
the
fraction
of that which is due
to him: I suppose that, for some arbitrary reasons, one keeps each year
the
fraction
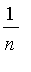 of this interest, so
that Paul, at the end of the first year, for example, must collect only
the
quantity
of this interest, so
that Paul, at the end of the first year, for example, must collect only
the
quantity
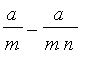 , this put,
if one pays him every year the sum
, this put,
if one pays him every year the sum
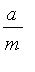 , and, consequently, more
than is due to him, and let the surplus be used to amortize the
capital,
one asks what this capital will become in the year
x .
, and, consequently, more
than is due to him, and let the surplus be used to amortize the
capital,
one asks what this capital will become in the year
x .
Let
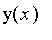 denote this capital in
the year
x . At the
end of the
year Paul will be due
denote this capital in
the year
x . At the
end of the
year Paul will be due
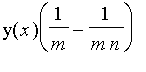 . Since
the sum
. Since
the sum
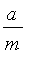 is paid, the capital
will be diminished by
is paid, the capital
will be diminished by
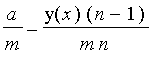 . We
have therefore
. We
have therefore
>
restart:
>
eqn11:=y(x+1)=y(x)-a/m+y(x)*(n-1)/(n*m);

The
initial condition is
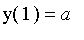 .
Therefore, the solution is given by
.
Therefore, the solution is given by
>
ans:=rsolve({eqn11,y(1)=a},y(x));
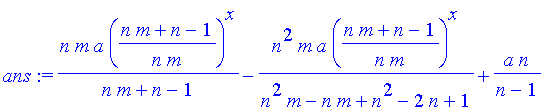
>
normal(ans);
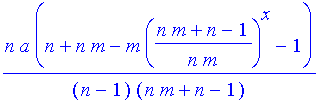
We
require when the capital
will vanish. That is, for what value of
x is
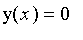 ?
?
>
vanish:=solve(ans=0,x);
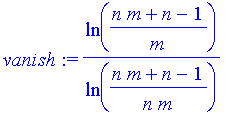
If
we substitute, as does
Laplace,
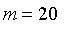 and
and
 then we find that this
occurs in 53.3 years.
then we find that this
occurs in 53.3 years.
>
subs({m=20,n=10},vanish);
>
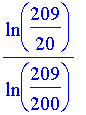
>
evalf(%);
>
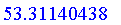
Addendum
to the
problem: A
person owes the sum a
, and wishes to release himself at the end of
h
years, so
that she owes nothing in the year
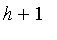 the interest being
always
the interest being
always
 of the quantity due;
the question is to find what
must she give for this each year.
of the quantity due;
the question is to find what
must she give for this each year.
With
Laplace, we let
p be what
she must
give each year.
>
eqn11a:=y(x+1)=y(x)*(1+1/m)-p;
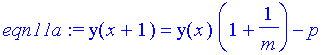
>
ans:=rsolve({eqn11a,y(1)=a},y(x));
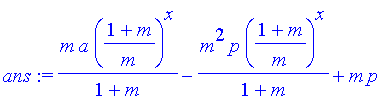
Laplace
puts
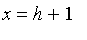 .
.
>
subs(x=h+1,ans);

>
ans2:=solve(%,p);
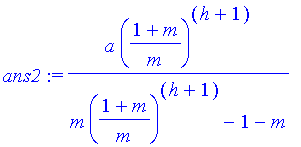
>
simplify(%);
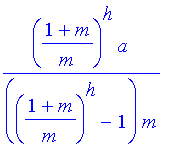
>
>
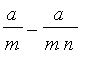 , this put,
if one pays him every year the sum
, this put,
if one pays him every year the sum
![]() .
Therefore, the solution is given by
.
Therefore, the solution is given by
![]() ?
?
![]() and
and
![]() then we find that this
occurs in 53.3 years.
then we find that this
occurs in 53.3 years.