recherch_xii.mws
Recherches sur
l'intégration des équations différentielles aux
différences finies, et sur leur usage dans la théorie des
hasards.
P.S. Laplace
PROBLEM
XII.
I
imagine a solid composed
of a number n
of faces perfectly equal, and which I
designate by
the numbers
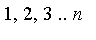 ;
I wish
to have the probability that, by
a number x
of casts, I will bring about these
n faces in
sequence in
the order
;
I wish
to have the probability that, by
a number x
of casts, I will bring about these
n faces in
sequence in
the order
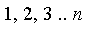 .
.
Let
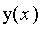 be the probability.
Laplace obtains the recurrence relation
be the probability.
Laplace obtains the recurrence relation
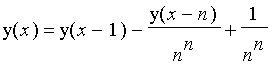 subject to the initial conditions
that
subject to the initial conditions
that
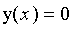 for
for
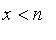 and
and
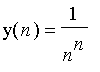 .
.
>
restart:
>
eqn12:=y(x)=y(x-1)-y(x-n)/n^n+1/n^n;
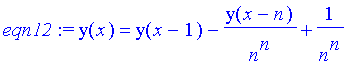
Example
1.
Laplace solves this in the case of
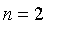 only. We must have
only. We must have
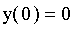 and
and
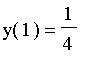 .
.
>
eqn12_2:=subs(n=2,eqn12);
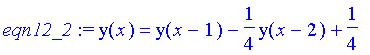
>
g2:=rsolve({eqn12_2,y(1)=0,y(2)=1/4},y(x),'makeproc'):
>
g2(x);
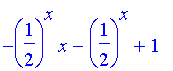
When
do we have an even
wager that the sequence 12 will appear? When
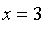 .
.
>
g2(3);
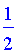
Example
2.
This problem is more difficult with
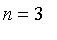 . The initial
conditions are that
. The initial
conditions are that
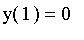 ,
,
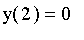 , and
, and
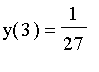 . It is
for reason of difficulty, I suspect,
that Laplace stopped with
. It is
for reason of difficulty, I suspect,
that Laplace stopped with
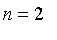 .
.
>
eqn12_3:=subs(n=3,eqn12);
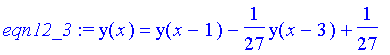
>
g3:=rsolve({eqn12_3,y(1)=0,y(2)=0,y(3)=1/27},y(x),'makeproc'):
>
factor(normal(g3(x)));
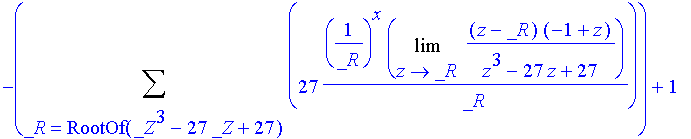
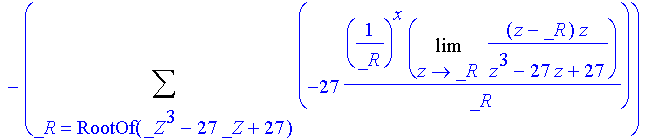
This
solution can be simplified
and the use of limits be avoided. Suppose
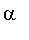 is a root of
is a root of
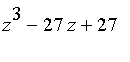 . Then
. Then
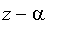 divides
divides
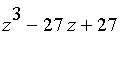 and
the factorization of this polynomial
is
and
the factorization of this polynomial
is
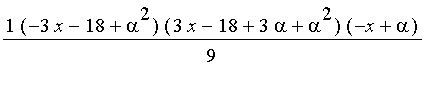
Thus
the other two roots
can be expressed in terms of the first as
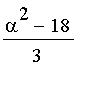 and
and
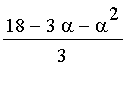 Moreover, we may rewrite
Moreover, we may rewrite
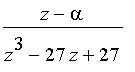 as
as
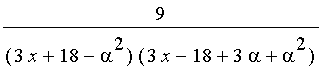 .
.
We
may then substitute this
new expression for
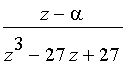 in the
solution given above.
in the
solution given above.
The
problem is completed
if we then sum over the three roots of
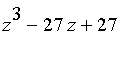 ,
substituting them successively for
,
substituting them successively for
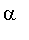 . Since the polynomial
is cubic, we can
find the roots exactly. These roots are
. Since the polynomial
is cubic, we can
find the roots exactly. These roots are
>
solve(z^3-27*z+27);
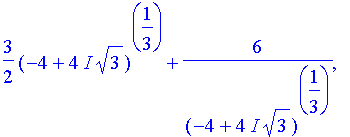
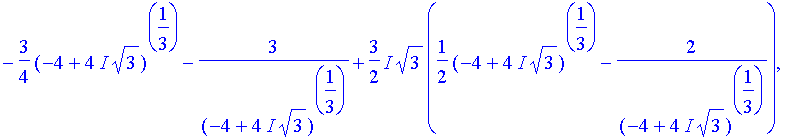
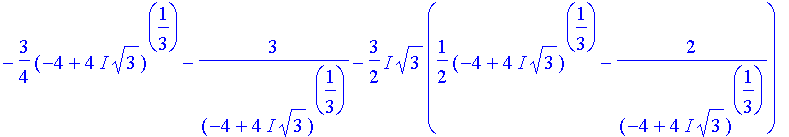
This
prospect is not fun.
An
alternative is to
compute the values recursively . We
do this
in general with the procedure
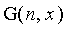 .
.
>
G:=proc(n,x::nonnegint) options remember;
> if x<n
then 0 elif x=n then 1/n^n else evalf(G(n,x-1)-G(n,x-3)/n^n+1/n^n); fi;
end:
For
example
, let's consider a die with 6 sides. In how many
tosses
do we have an even wager that the faces will appear in consecutive
order?
>
evalf(G(6,32342));
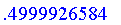
>
evalf(G(6,32343));
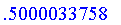
>
>
![]() only. We must have
only. We must have
![]() and
and
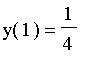 .
.
![]() .
.
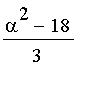 and
and
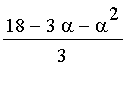 Moreover, we may rewrite
Moreover, we may rewrite
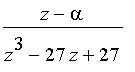 as
as
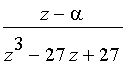 in the
solution given above.
in the
solution given above.
![]() .
.