recherch_xix.mws
Recherches sur
l'intégration des équations différentielles aux
différences finies, et sur leur usage dans la théorie des
hasards.
P.S. Laplace
PROBLEM
XIX.
I
suppose two players
A and B, with an equal number m
of écus, playing to this condition,
that the
one who loses will give an écu to the other; let the probability
of
A winning a trial be p
; let that of B be
q ; but let it
be able
to happen that any of them not win, and let the probability of this be
r .
This put,
we ask the probability that the game will end before or at the number
x
of
trials.
Consider
the probability
that player A has a stake k
at time x
. We may compute this through a Markov chain with
two
absorbing states, entered when the player either loses his stake or
gains
the entire stake of the other.
Example.
Suppose
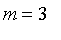 . The transition matrix
P is
clearly the one
having r on
the main diagonal excepting the corners,
q on the
sub-diagonal
and p on the
super-diagonal. The initial state
a is the
vector having
1 in the
. The transition matrix
P is
clearly the one
having r on
the main diagonal excepting the corners,
q on the
sub-diagonal
and p on the
super-diagonal. The initial state
a is the
vector having
1 in the
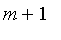 st position.
st position.
>
restart:
>
with(linalg):
Warning, the protected names norm and trace have been redefined and unprotected
>
P:=matrix(7,7,[[1,0,0,0,0,0,0],[q,r,p,0,0,0,0],[0,q,r,p,0,0,0],[0,0,q,r,p,0,0],[0,0,0,q,r,p,0],[0,0,0,0,q,r,p],[0,0,0,0,0,0,1]]);
![P := matrix([[1, 0, 0, 0, 0, 0, 0], [q, r, p, 0, 0,...](recherche_xix/recherch_xix3.gif)
>
a:=matrix(1,7,[0,0,0,1,0,0,0]);
![a := matrix([[0, 0, 0, 1, 0, 0, 0]])](recherche_xix/recherch_xix4.gif)
The
probability that player
A holds a stake k
at time x
is given by the value in the
k th
position of the
expression
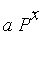 .
.
>
f:=x->evalm(a&*P&^x);

Thus,
for example, we can
examine the game after 4 matches.
>
f(4);
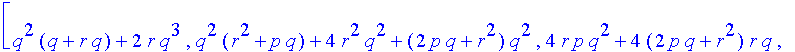
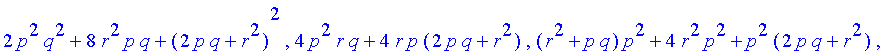
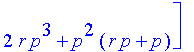
To
determine the probability
that the game end at or before time
x , it
suffices to
sum the first and last components. To this end we define the column
vector
b
with 1 in
its first and last position and zeros elsewhere.
>
b:=matrix(7,1,[1,0,0,0,0,0,1]):
Now,
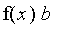 is this desired
probability.
is this desired
probability.
The
game ends at or before
time 4 with probability
>
evalm(f(4)&*b);
![matrix([[q^2*(q+r*q)+2*r*q^3+2*r*p^3+p^2*(r*p+p)]])...](recherche_xix/recherch_xix11.gif)
>
Suppose
now that
p ,
q and
r each
equal 1/3.
>
p:=1/3:q:=1/3:r:=1/3:
>
f:=x->evalm(a&*P&^x);
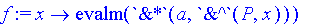
>
evalm(f(4)&*b);
![matrix([[4/27]])](recherche_xix/recherch_xix13.gif)
>
![]() is this desired
probability.
is this desired
probability.