recherch_xv.mws
Recherches sur
l'intégration des équations différentielles aux
différences finies, et sur leur usage dans la théorie des
hasards.
P.S. Laplace
PROBLEM
XV.
Three
players A, B, C,
of whom the respective abilities are represented by the letters p, q, r
play
together in a manner that, on a number x of trials, there lacks m to A,
n
to B and
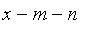 to C; we propose to
determine the respective probability
of these three players for winning.
to C; we propose to
determine the respective probability
of these three players for winning.
Let
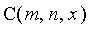 denote the
probability of C winning. Taking
denote the
probability of C winning. Taking
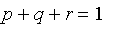 , we
must have
, we
must have
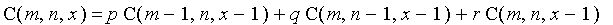
subject
to the conditions
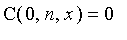 ,
,
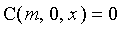 and
and
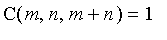 .
.
Laplace's
explicit solution
to this problem is quite cumbersome and it would be extremely difficult
to
extend his methods to 4 or more players. One "direct" technique to the
solution
is by a Markov chain. However, there will be
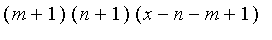 different states in this system. On the
other hand, computers allow us to make use of the recursive formulation
of
the problem.
different states in this system. On the
other hand, computers allow us to make use of the recursive formulation
of
the problem.
We
will let
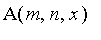 and
and
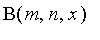 be the probability of
A and
B winning
respectively.
The recurrence relations for A
and B
are the same as for
C . Only the
boundary
conditions change.
be the probability of
A and
B winning
respectively.
The recurrence relations for A
and B
are the same as for
C . Only the
boundary
conditions change.
>
C:=proc(m,n,x)
> if (m=0
or n=0) then 0 elif x=m+n then 1 else
(C(m-1,n,x-1)+C(m,n-1,x-1)+C(m,n,x-1))/3
fi;
>
end:
>
A:=proc(m,n,x)
> if (n=0
or x=m+n) then 0 elif m=0 then 1 else
(A(m-1,n,x-1)+A(m,n-1,x-1)+A(m,n,x-1))/3
fi;
>
end:
>
B:=proc(m,n,x)
> if (m=0
or x=m+n) then 0 elif n=0 then 1 else
(B(m-1,n,x-1)+B(m,n-1,x-1)+B(m,n,x-1))/3
fi;
>
end:
Laplace
illustrates his
solution with the case where
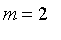 ,
,
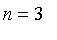 and
and
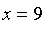 . Here we have
. Here we have
>
A(2,3,9);
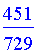
>
B(2,3,9);
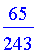
>
C(2,3,9);
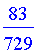
>
This
agrees with his solution.
The procedures generalize readily to 4 or more players.
>
![]() denote the
probability of C winning. Taking
denote the
probability of C winning. Taking
![]() , we
must have
, we
must have
![]() ,
,
![]() and
and
![]() .
.
![]() ,
,
![]() and
and
![]() . Here we have
. Here we have